Question

The gasses in a hair spray can are at temperature 300k and a pressure of 30 atm, it

the gasses in the can reach a pressure of 90 atm the can will explode. To what temperature must the
gusses be heated for the can to explode? Assume constant volume

Answer 1

900 K

Step-by-step explanation:

Recall the ideal gas law:

`\displaystyle PV = nRT`

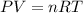
Because only pressure and temperature is changing, we can rearrange the equation as follows:

`\displaystyle (P)/(T) = (nR)/(V)`

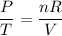
The right-hand side stays constant. Therefore:

`\displaystyle (P_1)/(T_1) = (P_2)/(T_2)`

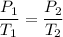
The can explodes at a pressure of 90 atm. The current temperature and pressure is 300 K and 30 atm, respectively.

Substitute and solve for T₂:

`\displaystyle \begin{aligned} \frac{(30\text{ atm})}{(300\text{ K})} & = \frac{(90\text{ atm})}{T_2} \\ \\ T_2 & = 900\text{ K}\end{aligned}`

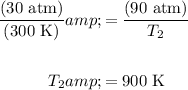
Hence, the temperature must be reach 900 K.