Question

In triangle RST, SQ=8 and QT=12. Find SW and UQ

Answer 1

Given:

In triangle RST, SQ=8 and QT=12.

To find:

The measure of sides SW and UQ.

Solution:

We know that centroid of a triangle is the intersection point of the medians and it divides each median in 2:1.

In the given figure SW and TU are medians and Q is the centroid. So,

`(SQ)/(QW)=(2)/(1)`

`(8)/(QW)=(2)/(1)`

`(8)/(2)=QW`

`4=QW`

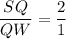
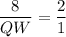
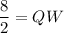
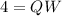
Now,

`SW=SQ+QW`

`SW=8+4`

`SW=12`

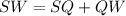
TU is a median. So,

`(QT)/(UQ)=(2)/(1)`

`(12)/(UQ)=(2)/(1)`

`(12)/(2)=UQ`

`6=UQ`

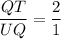
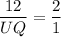
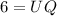
Therefore, the measure of SW is 12 units and the measure of UQ is 6 units.