Question

Write an equation of a line that goes thru the points (-2, 6) & (3, -4)

Answer 1

y= -2x +2

Explanation:

The equation of a line can be written in the form of y= mx +c, where m is the gradient and c is the y-intercept. This form is known as the slope-intercept form.

To find the value of m, use the gradient formula below:

`\boxed{gradient = (y1 - y2)/(x1 - x2) }`

`m = (6 - ( - 4))/( - 2 - 3)`

`m = (6 + 4)/( - 5)`

`m = (10)/( - 5)`

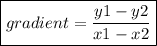
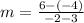
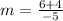
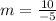
m= -2

Substitute m= -2 into the equation:

y= -2x +c

To find the value of c, substitute any pair of coordinates that the line passes through into the equation. Here, I am going to substitute the coordinates (3, -4).

y= -2x +c

When x= 3, y= -4,

-4= -2(3) +c

-4= -6 +c

c= -4 +6

c= 2

Thus, the equation of the line is y= -2x +2.