Answer:
The 32th term is 127.
Explanation:
Arithmetic sequence:
In an arithmetic sequence, the difference between consecutive terms is always the same. The general equation for an arithmetic sequence is given by:
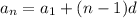
In which d is the common difference.
It can also be written as:
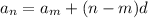
75th term is equal to 342, and the 4th term, 24, is equal to - 13.
This means that
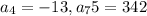 . We use this to find d. So
. We use this to find d. So
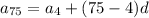

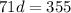
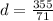
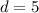
Find the value of the 32th term:
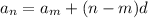
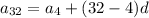
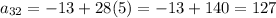
The 32th term is 127.