Question

CALCULUS: Which of the following functions grows the fastest as x goes to infinity?

A. 2^x
B. ln(x)
C. sin(x)
D. x^20 (I put this my first try & got it wrong)

I believe D is the right answer, but I got it wrong. Can someone please tell me why?

Answer 1

It is A. 2^x

Explanation:

For relative rates of growth, we know: Log < Poly < Exponential.

This rules out B, C, and D quickly. Although, if you do L'Hôpital's rule, it might seem like A & D are very comparable. However, if you continually took the derivative of 2^x and x^20, eventually x^20 would equal zero, while 2^x would still be a variable. So, you would have:

`\lim_(x \to \infty) (2^(x))/(0) =` ∞

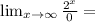When the limit of x as it approaches infinity is infinity, then f(x) grows at a faster rate than g(x).

Also, by looking at the graph (which is attached), you can see that 2^x grows faster than x^20.