The lateral surface area of the can is
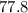 square inches and the total surface area of the can is
square inches and the total surface area of the can is
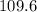 square inches, rounded to the nearest tenth.
square inches, rounded to the nearest tenth.
To find the lateral surface area (LSA) and the total surface area (TSA) of a cylinder (which the can is a common example of), you can use the following formulas:
Lateral Surface Area (LSA):
![\[ \text{LSA} = 2 \pi r h \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/tjors2g991g2e0cb87a4mdxkmeckpcr00h.png)
where
 is the radius of the base of the cylinder and
is the radius of the base of the cylinder and
 is the height.
is the height.
Total Surface Area (TSA):
![\[ \text{TSA} = \text{LSA} + 2(\pi r^2) \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/mgj1q4y82wh7r5z1c9ltq5re2uhxbuqiov.png)
The second term,
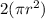 , represents the area of the two circular bases (top and bottom) of the cylinder.
, represents the area of the two circular bases (top and bottom) of the cylinder.
Step-by-step calculation:
1. Calculate the radius of the base of the can.
Since the diameter is given as \( 4.5 \) inches, the radius \( r \) is half of that:
![\[ r = (diameter)/(2) = (4.5)/(2) = 2.25 \text{ inches} \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/z6ka903dq8u89gx7ark4ovi5h2a1edgj70.png)
2. Calculate the Lateral Surface Area (LSA) using the radius and height.
The height
 is given as
is given as
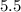 inches:
inches:
![\[ \text{LSA} = 2 \pi (2.25) (5.5) \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/m9sovrmtukn88yr0g2k3i57wnmat4rg8aw.png)
3. Calculate the area of one base of the cylinder.
![\[ \text{Base Area} = \pi r^2 = \pi (2.25)^2 \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/fne9dsu0otw7ss51wrynnta7e8t723p7as.png)
4. Calculate the Total Surface Area (TSA) by adding the LSA to twice the base area (since there are two bases):
![\[ \text{TSA} = \text{LSA} + 2(\text{Base Area}) \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/kl8p70rualprwunq1aq3pnt40b0u7hqyv1.png)
Now let's plug in the numbers and do the math:
For LSA:
![\[ \text{LSA} = 2 \pi (2.25) (5.5) \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/m9sovrmtukn88yr0g2k3i57wnmat4rg8aw.png)
![\[ \text{LSA} = 2 * 3.14159 * 2.25 * 5.5 \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/7vgehkwu9ib5bwhnyyc8vl52kmspfda781.png)
![\[ \text{LSA} \approx 77.8 \text{ square inches} \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/ea5tjjfhk2jjgyi9km16pn1124b95pah3g.png)
For Base Area:
![\[ \text{Base Area} = \pi (2.25)^2 \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/1rtu5iw3dqhkcda2qbngol31mxvxbnsd98.png)
![\[ \text{Base Area} = 3.14159 * 2.25 * 2.25 \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/fa4kgjojiy288ulrxari5hg9jd4d7xca6e.png)
![\[ \text{Base Area} \approx 15.9 \text{ square inches} \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/ij3lfuy653autfj1zw897jj4by30o9pt30.png)
For TSA:
![\[ \text{TSA} = \text{LSA} + 2(\text{Base Area}) \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/kl8p70rualprwunq1aq3pnt40b0u7hqyv1.png)
![\[ \text{TSA} = 77.8 + 2 * 15.9 \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/wjetre02d5vsac5z5bufa67r9wglo75pb4.png)
![\[ \text{TSA} \approx 109.6 \text{ square inches} \]](https://img.qammunity.org/2022/formulas/mathematics/middle-school/u0rsefb2n1mesoo5l3vlfw989nwtqsjdkd.png)
The lateral surface area of the can is
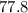 square inches and the total surface area of the can is
square inches and the total surface area of the can is
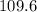 square inches, rounded to the nearest tenth.
square inches, rounded to the nearest tenth.