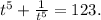Answer:
123
Explanation:
Squaring the given equation gives
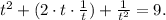
The
 and
and
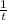 terms cancel out nicely, which is one of the reasons for squaring the equation.
terms cancel out nicely, which is one of the reasons for squaring the equation.
Simplifying gives
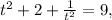
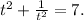
The question asks for
 so we can square the equation again and simplify to get higher powers into the expression:
so we can square the equation again and simplify to get higher powers into the expression:
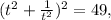
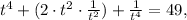

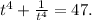
Multiplying this expression by
 to try and get a fifth power gives
to try and get a fifth power gives

The only thing left we need is
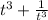 to subtract from this; we know everything else. Since
to subtract from this; we know everything else. Since
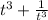 can be written as
can be written as
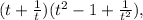 we can simply plug in the values we know for
we can simply plug in the values we know for
 and
and
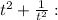
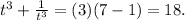
All that is left is to plug it in our equation here:
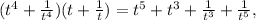
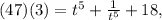
Multiplying and rearranging gives: