Answer:
Perimeter of one triangle is 65 dm
Perimeter of other triangle is 52 dm
Explanation:
Please remember the concept
If sides are in the ratio of a:b
Then the area in the ratio of
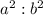
It is given sum of their perimeter is 117.
Let the small triangle has perimeter as x.
So, perimeter of big triangle is 117-x.
So, we can set up equation as
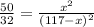
Cross multiply
50(117-x)^2 =32x^2
Expand the left side
50
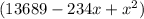 =
=
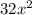
Distribute the left side
684450-11700x+
 =
=
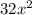
Subtract both sides
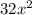 and rewrite it
and rewrite it
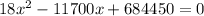
Solve this quadratic for x.
Divide both sides of the equation by 18 to simplify.
 -650 x+38025=0
-650 x+38025=0
Now, if possible let's factor
Find two integers whose multiplication is 38025 but adds to -650.
-65 and -585 works.
So, we can rewrite it as
(x -65)(x-585) =0
Solve them using zero product property
x=65, x=585
So, x=65 works here.
So, perimeter of one triangle is 65 dm
Perimeter of other triangle is 117-65= 52 dm