Answer:
The time it would take to fill up the truck is approximately 344 minutes
Explanation:
The given parameters of the truck are;
The volume of the water truck, V = 1,200 gallon
The rate at which water flows from the hose. m = Constant rate
The volume of water in the truck after t₁ = 10 minutes is V₁ = 65 gallons
The volume of water in the truck after t₂ = 15 minutes is V₂ = 82 gallons
Therefore, the rate at which water flows from the hose to the truck, 'm', is given by the equation for the slope of a straight (constant variation) line, as follows;
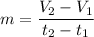
Therefore, we have;
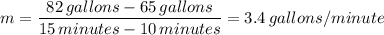
The point and slope form of the straight line equation relationship between the volume in the tank and the time of flow is given as follows;
V - 82 = 3.4 × (t - 15)
Therefore, the slope and intercept form of the equation is given as follows;
V = 3.4·t - 15 × 3.4 + 82 = 3.4·t + 31
∴ V = 3.4·t + 31
When the tank is filled, V = 1,200 gallons, therefore, we have;
1,200 = 3.4·t + 31
3.4·t = 1,200 - 31 = 1,169
t = 1,169/3.4 = 5845/17 = 343.
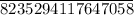
The time it would take to fill up the truck, t = 343.
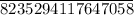 minutes ≈ 344 minutes.
minutes ≈ 344 minutes.