Answer:
Based on the confidence interval, the method appears to not bring expected results
Explanation:
The given parameters are;
The number of babies in the study, n = 620 babies
The number of girls in the study sample = 341 girls
The proportion of girls in the study sample,
 = 341/620 = 0.55
= 341/620 = 0.55
At 99% confidence level, we have the critical z = 2.576;
The confidence interval is given by the following formula;
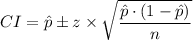
Plugging in the values of the variables, we get;
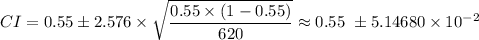
Therefore, 0.498532 < p < 0.601468
Based on the result of the confidence interval, we can be 99% sure that the true mean is between 0.498532 and 0.601468, therefore, given that the range includes a true mean of 0.5 or 50% probability of conceiving a girl, which is the percentage predicted by genetics, the method appears ineffective