Answer:
Base = 7.1m
Height = 14.2m
Explanation:
Let's take the base as 'x'.
And the height is twice the base so it is 2 × x which is 2x.
Then, the formula for finding area of a triangle is:
Area of a triangle =
 × base × height
× base × height
From this equation we will be able to find the value of 'x'.
The area is 50
 . Now substitute all the terms into the equation.
. Now substitute all the terms into the equation.
50 =
 × x × 2x
× x × 2x
50 =
 ×
×
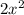
50 =

The '2' in the numerator and denominator can be cut off.
 = 50
= 50
x =
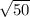
x = 7.07 = 7.1m ( to the nearest tenth )
So when the base is 7.07 the height, as mentioned, is twice of base, 2x. We have the value of x so just substitute the value of x in 2x.
2 × 7.1 = 14.2m