Answer:
The correct option is;
D. (x - 5)·(x + 2)·(x + 1)
Explanation:
The Rational Root theorem is expressed mathematically as follows;
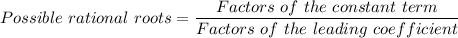
The given polynomial is presented as follows;
x³ - 2·x² - 13·x - 10
A factor of the polynomial = (x + 1)
The factors of the constant term, -10 = -10, -5, -2, -1, 10, 5, 2, and 1
The factors of the leading coefficient, (the coefficient of the variable having the highest degree or power, x³) = 1
Given that (x + 1) is a known factor, the other two factors are either (x + 5) and (x - 2) or (x - 5) and (x + 2)
The option, that combines (x + 1) and the other two factor combination is (x - 5)·(x + 2)·(x + 1)
∴ The solution which meets the condition is (x - 5)·(x + 2)·(x + 1)
We check;
(x - 5)·(x + 2)·(x + 1) = x³ - 2·x² - 13·x - 10