Question

determine the value of m and n for mx^3 +20x^2+ nx-36 when divided by (x+1) gives remainder 0 and when divided by (x-2) gives remainder of 45.​

Answer 1

Given:

The given polynomial is

`mx^3+20x^2+nx-36`

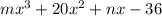
When it divided by (x+1) gives remainder 0 and when divided by (x-2) gives remainder of 45.

To find:

The values of m and n.

Solution:

According to the remainder theorem, if a polynomial P(x) is divided by (x-c), then the remainder is P(c).

Let the given polynomial be P(x).

`P(x)=mx^3+20x^2+nx-36`

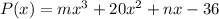
When it divided by (x+1) gives remainder 0. So, P(-1)=0.

`P(-1)=m(-1)^3+20(-1)^2+n(-1)-36`

`0=-m+20-n-36`

`0=-m-n-16`

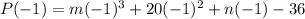
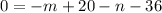
`m+n=-16` ...(i)

When P(x) is divided by (x-2) gives remainder of 45. So, P(2)=0

`m(2)^3+20(2)^2+n(2)-36=45`

`8m+80+2n-36=45`

`8m+2n+44=45`

`8m+2n=45-44`

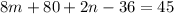
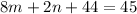
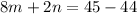
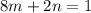`8m+2n=1` ...(ii)

Multiply 2 on both sides of (i).

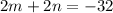`2m+2n=-32` ...(iii)

Subtract (iii) from (ii).

`6m=33`

`m=(33)/(6)`

`m=5.5`

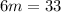
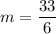
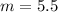
Putting m=5.5 in (i), we get

`5.5+n=-16`

`n=-16-5.5`

`n=-21.5`

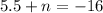
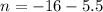
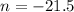
Therefore, the values of m and n are 5.5 and -21.5 respectively.