Answer:
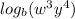
Explanation:
To write the expression as a single logarithm, or condense it, use the properties of logarithms.
1) The power property of logarithms states that
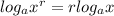 . In other words, the exponent within a logarithm can be brought out in front so it's multiplied by the logarithm. This means that the number in front of the logarithm can also be brought inside the logarithm as an exponent.
. In other words, the exponent within a logarithm can be brought out in front so it's multiplied by the logarithm. This means that the number in front of the logarithm can also be brought inside the logarithm as an exponent.
So, in this case, we can move the 3 and the 4 inside the logarithms as exponents. Apply this property as seen below:
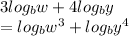
2) The product property of logarithms states that
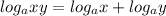 . In other words, the logarithm of a product is equal to the sum of the logarithms of its factors. So, in this case, write the expression as a single logarithm by taking the log (keep the same base) of the product of
. In other words, the logarithm of a product is equal to the sum of the logarithms of its factors. So, in this case, write the expression as a single logarithm by taking the log (keep the same base) of the product of
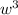 and
and
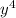 . Apply the property as seen below and find the final answer.
. Apply the property as seen below and find the final answer.
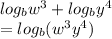
So, the answer is
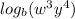 .
.