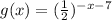Complete Question:
g(x), represents transformations on the parent function of
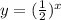 .
.
Write the equation for g (x ) with the following transformations:
Reflect over y-axis, and shift right 7
Answer:
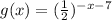
Explanation:
Given
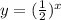
Represent the function as:
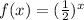
Taking the transformations, one after the other:
Reflect over the y-axis.
This is represented by the rule: (x,y) ==> (-x,y)
So, we have:
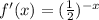
Shift right 7 units
This is represented by (x,y) = (x - b, y)
Where b represents the number of units
So, we have:
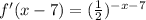
Hence: