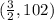Answer:
Explanation:
Given
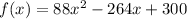 --- Missing from the question
--- Missing from the question
Required
The symmetry
First, we express f(x) as:
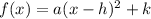
Where the symmetry is: (h, y) and x = h
Equate f(x) to 0
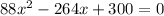
Subtract 300 from both sides
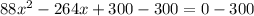
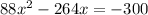
Factorize
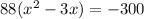
On the left-hand side, the coefficient of x is -3.
Divide by 2 and add the square to both sides.
So, we have:
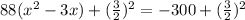
Multiply the new terms by 88 (to make it factorizable)
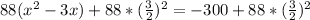
Factorize
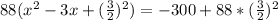
The quadratic expression in the bracket is a perfect square. This gives:
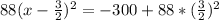
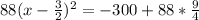
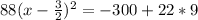
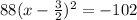
Add 102 to both sides
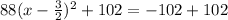
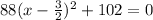
Equate to y
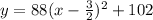
Recall that:
The symmetry is: (h, y)
By comparison with
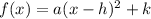 and x = h
and x = h
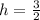
So:
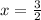
Substitute
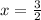 in
in
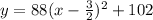
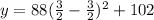
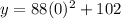
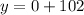
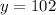
So, the symmetry is: