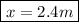Question

Two point charges of 9μC and 4μC are placed a distance of 4 m apart.

1) Calculate the magnitude of the force, in Newtons, on a positive 5μC charge at the midpoint between the two charges.
2) Find the point, measured in meters from the 9μC charge, between the two charges where the force on the 5μC charge is 0?

Answer 1

Hi there!

1)

Since the charge placed in the middle is positive, we know that the particle is being repelled.

The particle experiences a greater repelling force by the 9μC charge. We can use the equation for electric force:

`F_E = (kq_1q_2)/(r^2)`

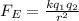
k = Coulomb's Constant

q₁, q₂: Charges (C)
r = distance between charges (m)

This is a VECTOR quantity, so we must subtract the forces since they point in opposite directions.

Force from 9μC particle:

`F_E = (k(.000005)(.000009))/(2^2) = .101\\\\`

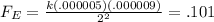
Force from 4μC particle:

`F_E = (k(0.000005)(0.000004))/(2^2) = 0.0450`

Subtract:

`.101 - 0.0450 = \boxed{0.561 N}`

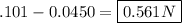
2)

We can find a position by setting the two equations equal to one another. (Both repelling forces must be EQUAL for the force = 0 N)

Let the distance between the 9μC and 5μC charge equal 'x', and the distance between the 4μC and 5μC charge equal '4 - x'.

`(k(0.000009)(0.000005))/(x^2) = (k(0.000004)(0.000005))/((4 - x)^2)`

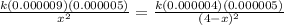
Cancel out 'k' and the 5μC value.

`(0.000009)/(x^2) = (0.000004)/((4 - x)^2)`

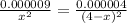
Solve for 'x' using a graphing utility.

`\boxed{x = 2.4 m}`