Answer:
The possible equation is; T(t) = 20 + 80·
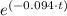
The horizontal asymptotes is Lim(t → ∞), T → 20°C
The vertical asymptote is Lim(t → 0) T → 100°C
Explanation:
The given parameters are;
The temperature of the house = 20°C
The initial temperature of the tea = 100°C
The temperature of the tea after 5 minutes = 70°C
From Newton's law of cooling, is given as follows;
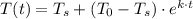
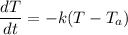
Where;
T(t) = The temperature after time, t =
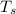 =The room temperature = 20°C
=The room temperature = 20°C
T₀ = The initial temperature of the tea = 100°C
k = Constant
T(5) = 70°C, therefore, we have;
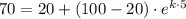
50/80 =
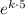
5·k = ㏑(5/8)
k = ㏑(5/8)/5 ≈ -0.094
Therefore, the possible equation is given as follows;
T(t) = 20 + 80·
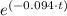
The asymptotes are Lim(t → ∞), T → 20°C and Lim(t → 0) T → 100°C