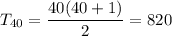Answer:
a) 253
b) 66
c) 496
d) 820
Step-by-step explanation:
Triangular numbers : pattern of numbers that form equilateral triangles. Each subsequent number in the sequence adds a new row of dots to the triangle.
nth triangular number formula:
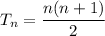
a) if n = 22
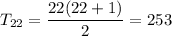
b) if n = 11
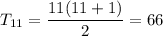
c) if n = 31
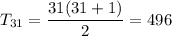
d) if n = 40