Answer:
Greater than 1250
x > 1250
Explanation:
Base on the revenue equation and cost equation , we can infer that the company make a profit when x > 1250
Important Given Information:
The revenue equation is
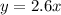
Cost equation is
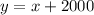
When the company makes profit only when:
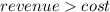
Let's frame inequality using:
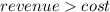
Replace the revenue equation and cost equation
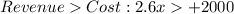
Now Let's solve the inequality for x
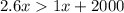
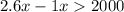
![[2.6x-1x=1.6x]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/u9n3448i7ue4j733ot05.png)
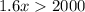
Divide both sides by 1.6 ( what you do on one side do to the other)
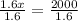
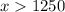
Hence, the company makes profit when x is greater than 1250
[RevyBreeze]