Question

Help pls ! This is trigonometric function

Answer 1

Part A: The amplitude
`\displaystyle r`is
`\displaystyle 4.`

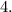
Part B: The period of
`\displaystyle r`is
`\displaystyle \pi.`

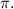
Part C: The equation of the midline of
`\displaystyle r`is
`\displaystyle y = 1.`

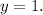
Step-by-step explanation:

`\displaystyle \boxed{r(x) = -4cos\:(2x - (\pi)/(2)) + 1} \\ \\ r(x) = Acos(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \\ Wavelength\:[Period] \hookrightarrow (2)/(B)\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow 1 \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \hookrightarrow \boxed{(\pi)/(4)} \hookrightarrow ((\pi)/(2))/(2) \\ Wavelength\:[Period] \hookrightarrow (2)/(B)\pi \hookrightarrow \boxed{\pi} \hookrightarrow (2)/(2)\pi \\ Amplitude \hookrightarrow 4`

OR

`\displaystyle r(x) = Asin(Bx - C) + D \\ \\ Vertical\:Shift \hookrightarrow D \\ Horisontal\:[Phase]\:Shift \hookrightarrow (C)/(B) \\ Wavelength\:[Period] \hookrightarrow (2)/(B)\pi \\ Amplitude \hookrightarrow |A| \\ \\ Vertical\:Shift \hookrightarrow 1 \\ Horisontal\:[Phase]\:Shift \hookrightarrow 0 \\ Wavelength\:[Period] \hookrightarrow (2)/(B)\pi \hookrightarrow \boxed{\pi} \hookrightarrow (2)/(2)\pi \\ Amplitude \hookrightarrow 4`

Keep in mind that although this IS a sine function, if you plan on writing your equation as a function of cosine, then there WILL be a horisontal shift, meaning that a C-term will be involved. As you can see, the centre photograph displays the trigonometric graph of
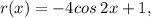`\displaystyle r(x) = -4cos\:2x + 1,`in which you need to replase "sine" with "cosine", then figure out the appropriate C-term that will make the graph horisontally shift and map onto the sine graph [photograph on the left], accourding to the horisontal shift formula above. Also keep in mind that the −C gives you the OPPOCITE TERMS OF WHAT THEY REALLY ARE, so you must be careful with your calculations. So, between the two photographs, we can tell that the cosine graph [centre photograph] is shifted
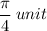`\displaystyle (\pi)/(4)\:unit`to the left, which means that in order to match the sine graph [photograph on the left], we need to shift the graph FORWARD
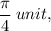`\displaystyle (\pi)/(4)\:unit,`which means the C-term will be positive, and by perfourming your calculations, you will arrive at
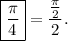`\displaystyle \boxed{(\pi)/(4)} = ((\pi)/(2))/(2).`So, the cosine graph of the sine graph, accourding to the horisontal shift, is
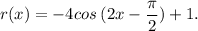`\displaystyle r(x) = -4cos\:(2x - (\pi)/(2)) + 1.`So, with all that being said, to find the period, again, take a look at the above information next to
`\displaystyle Wavelength\:[Period].`Now, the amplitude is obvious to figure out because it is the A-term. Moreover, the midline is the centre of your graph, also known as the vertical shift, which in this case the centre is at
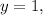`\displaystyle y = 1,`in which each crest is extended four units beyond the midline, hence, your amplitude. Now, there is one more piese of information you should know -- the sine graph in the photograph farthest to the right is the OPPOCITE of the sine graph in the photograph farthest to the left, and the reason for this is because of the negative inserted in front of the amplitude value. Whenever you insert a negative in front of the amplitude value of any trigonometric equation, the whole graph reflects over the midline. Keep this in mind moving forward. Now, with all that being said, no matter how far the graph shifts vertically, the midline will ALWAYS follow.

I am delighted to assist you at any time.

Answer 2

Amplitude: 4

Period: π

midline: y = 1

Explanation:

r(x) = -4 sin(2x) + 1

r(x) = a sin(bx + c) + d where |a| is the amplitude and |b| for the period

a = -4 |a| = 4 : Amplitude = 4

b = 2 |b| = 2 period of sin(x) = 2π

period of sin(bx + c) = 2π/|b| = 2π/2 = π

range of sin(2x) ... -1 ≤ sin(2x) ≤ 1

range of -4 sin(2x) + 1: -4+1 ≤ -4 sin(2x) + 1 ≤ 4+1

-3 ≤ -4 sin(2x) + 1 ≤ 5

midline: y = (-3 + 5) / 2 = 1 y = 1