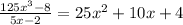Answer:
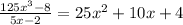
Explanation:
Given
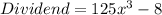
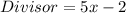
Required
Determine the quotient
See attachment for complete process.
First, divide 125x^3 by 5x
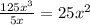
Write
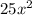 at the top
at the top
Multiply
 by
by
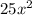

Subtract from 125x^3 - 8
i.e.
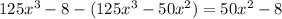
Step 2:
Divide 50x^2 by 5x
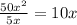
Write
 at the top
at the top
Multiply
 by
by

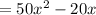
Subtract from 50x^2 - 8
i.e.
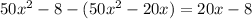
Step 3:
Divide 20x by 5x
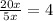
Write
 at the top
at the top
Multiply
 by
by

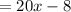
Subtract from 20x - 8
i.e.
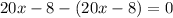
Hence: