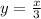Question

Please help fast! I have no idea what I'm supposed 2 do

Answer 1

Constant of proportionality:
`(1)/(3)`

Equation:
`y=(1)/(3)x`

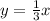
Explanation:

The constant of proportionality is the ratio between y and x, according to the following formula

constant of proportionality = k = y/x

Take the given pairs and replace the data.

1.


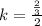
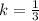
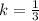
`k=((2)/(3))/(2)`

`k = (1)/(3)`

2.

`k = (1)/(3)`

3.

`k=((10)/(3))/(10)`

`k = (1)/(3)`

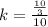
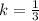
4.

`k = (4)/(12)`

`k = (1)/(3)`

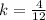
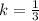
As you can see, the constant is the same for all the pairs.

constant of proportionality =
`(1)/(3)`

Now, in order to know the equation make a graph of the given data.

The graph is in the picture

Since it is a line, use the equation of the line in point slope form

`y- { y }_( 1 ) = m \left( x- { x }_( 1 ) \right)`

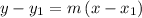
where (x1, y1) = any pair of the data

m = slope = constant of proportionality

Replace the data in the equation

`y-1 = ( 1 )/( 3 ) \left( x-3 \right)`

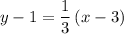
Use the distributive property to multiply
`(1)/(3)` by x - 3

`y-1=(1)/(3)x-1`

Add 1 to both sides

`y = ( 1 )/( 3 ) x-1+1`

Add −1 and 1 to get 0

`y=(1)/(3)x`

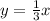
or

`y=(x)/(3)`