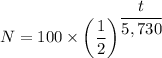Question

For each carbon-14 atom, there are approximately 10^12 carbon-12 atoms. This ratio is constant in each organism. The carbon-12 remains constant but the carbon-14 decays. Suppose a piece of wood is analysed, and it contains 10^14 carbon-12 atoms and 40 carbon-14 atoms.

1) Determine how many carbon-14 atoms were present in the wood when it died.

2) Use the half life of carbon-14 atoms to obtain a function to model the number N of carbon-14 atoms present in the wood (t) years after it died

Answer 1

1) There are 100 carbon-14 atoms in the wood when it died

2) A function that models the number 'N' of carbon-14 atoms present in the wood (t) years after it died is presented as follows;

`N = 100 * \left ((1)/(2) \right )^{(t)/(5,730) }`

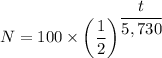
Explanation:

The given parameters are;

The number of carbon-12 for each carbon-14 atom ≈ 10¹² carbon-12 atoms

The number of carbon-12 in the piece of wood = 10¹⁴ carbon-12 atoms

The number of carbon-14 in the piece of wood = 40 carbon-14 atoms

The number of carbon-12 in an organism = Constant

The number of carbon-14 in an organism = Decays

1) Given that the number of carbon-12 in an organism is constant, and there are 10¹² carbon-12 atoms per each carbon-14 atom, therefore, we have;

The number of carbon-12 atoms in the wood when it died = 10¹⁴ carbon-12 atoms

The number of carbon-14 atoms in the wood when it died = (10¹⁴ carbon-12 atoms)/(10¹² carbon-12 atoms/(carbon-14 atom)) = 100 carbon-14 atoms

The number of carbon-14 atoms in the wood when it died = 100 carbon-14 atoms

2) The half life of a radioactive isotope is given by the following formula;

`N(t) = N_0 \cdot \left ((1)/(2) \right )^{\frac{t}{t_{(1)/(2) }} }`

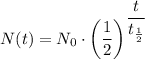
The half life of carbon-14 atoms,
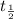`t_{(1)/(2) }` ≈ 5,730 years

N₀ = The amount of carbon-14 present in the wood when it died = 100 carbon-14 atoms

Therefore, we have;

The number, N, of carbon-14 atoms present in the wood (t) years after it died is given as follows;

`N = 100 * \left ((1)/(2) \right )^{(t)/(5,730) }`