Answer:
2x + 3y - 4 = 0
Explanation:
Equation of the line → 2x - 3y + 4 = 0
3y = 2x + 4
y =
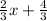
Slope of this line 'm' =
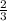
y-intercept of this line → y =
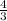 Or
Or
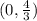
Let the equation of the line is,
y = m'x + b'
By the property of perpendicular lines,
m × m' = -1
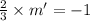
m' =
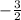
Equation of the perpendicular line will be,
y =
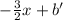
Since this line passes through
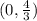 ,
,
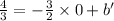
b' =
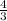
Therefore, equation of the perpendicular line will be,
y =
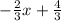
3y = -2x + 4
2x + 3y - 4 = 0