Answer:
3.5 × 10⁻³ Ω
Explanation:
The resistance of a conductor is calculated by the formula:
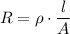
- where R = electric resistance (Ω), ρ = resistivity (Ω · m), l = length of the wire (m), A = area of the cross-section of the wire (m²)
Let's start by converting the diameter of the copper wire to meters.
Since we want the radius of the cross-section, we will divide .002 m by 2.
The radius of the copper wire is .001 m. We can calculate the area of the circular cross-section by using the formula:
The area of the cross-section is π · 10⁻⁶ m².
The length of the wire is 0.65 m long. We do not have to convert units for the length of the wire since it is already in the SI units: meters.
Assuming the copper wire is at 20°C, we know that its resistivity is 1.7 · 10⁻⁸ Ω · m.
Using these three variables, we can solve for R in the formula for electric resistance.
- ρ = 1.7 · 10⁻⁸ Ω · m
- l = 0.65 m
- A = π · 10⁻⁶ m²
Substitute these values into the equation.
Notice how the unit m² cancels out, leaving us with Ω (units of electrical resistance).
The electric resistance of a copper wire 0.65 m long with a radius of .001 m is .0035 ohms (Ω), or 3.5 × 10⁻³ Ω.