Question

How many and what type of solution(s) does the equation have?8p^2=24p−10

Answer 1

2 real solutions

Explanation:

to understand this

you need to know about:

• discriminant
• PEMDAS

tips and formulas

• 
  `D=b^(2)-4ac`
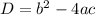
• D>0 (2 real solutions)
• D=0 (1 real solution)
• D<0 (2 imaginary solutions) or (no real solutions)

let's solve:

• move left hand side expressions to right hand side and change its sign:8p²-24p+10=0
• divide both sides by 2 :4p²-12p+5=0

the quadratic equation standard form is

• ax²+bx+c=0

therefore we get

• a=4
• b=-12
• c=5

-------------------------------

1. substitute the value of a,b and c into the discriminant: D=-12²-4.4.5
2. simplify square:144-4.4.5
3. simplify multiplication:144-80
4. simplify substraction:64

since we got D>0

therefore

the quadratic equation has 2 real solutions