Question

Given the function g(x)= -x^2 + x + 5, determine the average rate of change of the function over the interval -4 ≤ x ≤ 3.​

Answer 1

The average rate of change is 2.

Explanation:

We are given the function:

`g(x)=-x^2+x+5`

And we want to find the average rate of change over the interval:

`-4\leq x\leq 3`

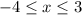
The average rate of change is synonymous with the slope. So, we will evaluate the function at its endpoints and find the slope between them.

Our first endpoint is given by:

`g(-4)=-(-4)^2+(-4)+5=-15`

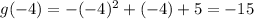
And our second endpoint is given by:

`g(3)=-(3)^2+(3)+5=-1`

This gives us two points (-4, -15) and (3, -1). The average rate of change will be the slope between them. Thus:

`\displaystyle ARC=(-1-(-15))/(3-(-4))=(14)/(7)=2`

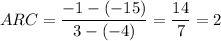
The average rate of change is 2.