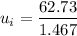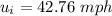The question is incomplete. The complete question is :
A car is stopped at a traffic signal. A second car rear-ends the first car. From the crush of the two vehicles, it is estimated that the second car was traveling at 15 mph when it impacted the first car. If the second car laid down 166 feet of skid marks before the crash took place, how fast was the second car traveling when its brakes were locked up? The approach to the intersection where the accident took place is on a 2.5 percent downgrade. Assume the AASHTO recommended deceleration rate of
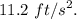
Solution :
From the equation, the skid distance is given by
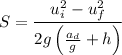
Here,
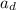 = deceleration rate,
= deceleration rate,
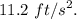
h =
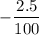 = -0.025
= -0.025
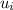 = initial speed of the car
= initial speed of the car
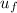 = speed when impacted
= speed when impacted
Therefore,
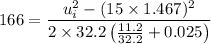
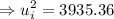
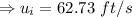
or