Question

Demand for fasteners at W.W. Grainger is 20,000 boxes per month. Holding cost at Grainger is 20 percent per year. Each order incurs a fixed cost of $400. The supplier offers an all unit discount pricing scheme with a price of $5 per box for orders under 30,000 and a price of $4.90 for all orders of 30,000 or more. How many boxes should Grainger order per replenishment

Answer 1

Given :

The annual demand, D =
`$200000 * 12$`

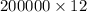
= 240,000

The ordering cost, S = $ 400

Holding cost, H = 20 percent per year

The EOQ for each year,

`$EOQ=\sqrt{(2DS)/(H)}$`

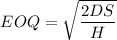
Under 30000, the cost = 5, Holding cost = 5 x 0.2 = 0

`$EOQ=\sqrt{(2* 240000 * 400)/(1)}$`

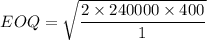
= 13856.41

= 13856 (approx.)

It is feasible as it is not with in range of 30000 or more.

So calculating total cost at order quantity, Q = 13856 and 30000

Therefore total cost = purchase cost + annual ordering cost + annual holding cost.

`$=(CD)+(Q)/(2)H+(D)/(Q)S$`

Q = 13856

Total cost =
`$(5* 240000)+((240000)/(13856))* 400+((12856)/(2))* 1$`

= 1213856

Q = 30000

Total cost =
`$(4.9* 240000)+((240000)/(30000))* 400+((30000)/(2))* 0.98= 1193900$`

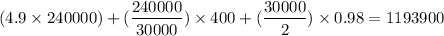
Total cost is less than Q = 30000

Order quantity = 30000 boxes