Answer:
They should deposit $105 every month so that they reach their goal.
Step-by-step explanation:
Given - Liz and Bob just had a baby named Isabelle, and they want to
save enough money for Isabelle to go to college. Assume that
they start making monthly payments when Isabelle is 5 into an
ordinary annuity earning 3.79%, and they calculate that they will
need $21,200.00 by the time Isabelle turns 18.
To find - How much should they deposit every month so that they reach
their goal.
Proof -
We know the formula -
Future value =
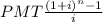
Here , we have
i =
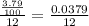
n = 12×(18 - 5) = 156
Future value = 21,200.00
∴ we get
21,200.00 =
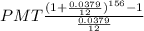
⇒21,200 =
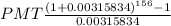
⇒21,200 =
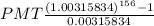
⇒21,200 =
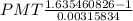
⇒21,200 =
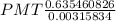
⇒21,200 = PMT(201.2008924)
⇒PMT =
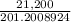
⇒PMT = 105.3673259 ≈ $105
∴ we get
They should deposit $105 every month so that they reach their goal.