Question

-x^2+4x-8
axis of symmerty​

Answer 1

`\boxed {\boxed {\sf x=2}}`

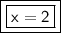
Explanation:

The axis of symmetry can be calculated using the formula:

`x=(-b)/(2a)`

First we must determine a and b from the quadratic:
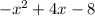`-x^2+4x-8`. This is in standard form, with the highest power first in descending order.

Standard form is also:
`ax^2+bx+c`

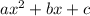
If we compare this to the quadratic given, we can conclude that:

`a= -1 \\b= 4 \\c= -8`

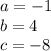
Substitute the values for a and b into the formula.

`x= (-(4))/(2(-1))`

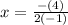
Multiply in the denominator.

`x=\frac {-4}{-2}`

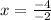
Divide.

`x=2`

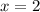
This can also be determined from the graph. It is the x-coordinate of the vertex or the maximum/minimum. It divides the quadratic into 2 symmetrical halves.