Answer:
a) 400 meters
b) 67 meters
c) 124.790 meters
Explanation:
Given data :
g1 = - 0.4 %
g2 = +2 %
change of grade of sag curve ( a ) = 0.6 %
Elevation of PVI ( h2 ) = 124.80 m
a) compute the length of the curve using the relation below
a =
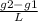 . hence ; L = ( g2 - g1 ) / a
. hence ; L = ( g2 - g1 ) / a
L = ( 2 -(-0.4 ) / 0.6
= 2.4 / 0.6 = 4
= 400 meters
b) compute the elevation of the lowest point of the curve
slope of the vertical curve = 0
0 = 2ax l + b
= 2(
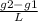 ) x + g1
) x + g1
∴ x =
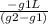 = ( 0.4 * 4 ) / ( 2 + 0.4 ) = 1.6 / 2.4 = 0.67 stations
= ( 0.4 * 4 ) / ( 2 + 0.4 ) = 1.6 / 2.4 = 0.67 stations
therefore x ( elevation of the lowest point ) = 67 meters
C) compute the elevation at Sta. 12 + 125.60
Given that the rate of change of elevation is the same at all points
=
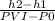 = 0.4 -------- ( 1 )
= 0.4 -------- ( 1 )
where h2 = 124.80
h1 = ? ( elevation of p0 ) at 12 + 125.60
PVI = 12 + 150.06
p0 = 12 + 125.60
back to the above equation
- h1 = 0.4 ( PVI - P0 ) - h2
= 0.4 ( 12.150 - 12.1256 ) - 124.80
-h1 = -124.790
hence h1 = 124.790 m