Answer:
1537 voters should be polled.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:

95% confidence level
So
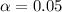 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
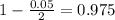 , so
, so
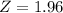 .
.
20% of voters are in favor of certain legislation.
This means that
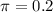
How many voters should be polled in order that the probability is at least .95 that fA(n) differs from 0.20 by less than 0.02
This is n for which M = 0.02. So

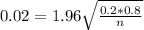
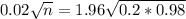
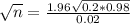
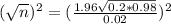
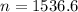
Rounding up
1537 voters should be polled.