Question

Please someone helpme

Answer 1

`\displaystyle t = (2 \pi)/(3), \ (4 \pi)/(3)`

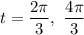
General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Functions
• Function Notation
• [Interval Notation] - [Brackets] imply inclusive, (Parenthesis) imply exclusive

Pre-Calculus

• Unit Circle

Calculus

Derivatives

Derivative Notation

The definition of a derivative is the slope of the tangent line

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Trig Derivative:
`\displaystyle (d)/(dx)[sinu] = u'cosu`

Explanation:

Step 1: Define

[Given] q(t) = t + 2sint

[Given] Interval [0, 2π]

[Solve] q'(t) = 0

• Horizontal tangent line have a slope of 0

Step 2: Differentiate

1. [Derivative] Basic Power Rule/Trig Derivative [Derivative Prop - Add]:
   `\displaystyle q'(t) = 1 \cdot t^(1 - 1) + 1 \cdot 2cost`
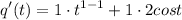
2. [Derivative] Simplify exponent:
   `\displaystyle q'(t) = 1 \cdot t^(0) + 1 \cdot 2cost`
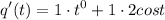
3. [Derivative] Evaluate exponent:
   `\displaystyle q'(t) = 1 \cdot 1 + 1 \cdot 2cost`
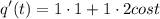
4. [Derivative] Multiply:
   `\displaystyle q'(t) = 1 + 2cost`

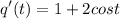
Step 3: Solve

1. [Derivative] Substitute in function value:
   `\displaystyle 0 = 1 + 2cost`
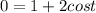
2. [Subtraction Property of Equality] Isolate t term:
   `\displaystyle -1 = 2cost`
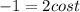
3. Rewrite:
   `\displaystyle 2cost = -1`
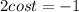
4. [Division Property of Equality] Isolate trig t term:
   `\displaystyle cost = (-1)/(2)`
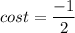
5. [Equality Property] Inverse Trig:
   `\displaystyle t = cos^(-1)((-1)/(2))`
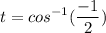
6. Evaluate [Unit Circle, Interval]:
   `\displaystyle t = (2 \pi)/(3), \ (4 \pi)/(3)`

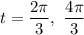
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Derivatives

Book: College Calculus 10e