Question

You are in charge of purchases at the student-run used-book supply program at your college, and you must decide how many introductory calculus, history, and marketing texts should be purchased from students for resale. Due to budget limitations, you cannot purchase more than 1050 of these textbooks each semester. There are also shelf-space limitations: Calculus texts occupy 2 units of shelf space each, history books 1 unit each, and marketing texts 5 units each, and you can spare at most 1,800 units of shelf space for the texts. If the used book program makes a profit of $10 on each calculus text, $4 on each history text, and $8 on each marketing text, how many of each type of text should you purchase to maximize profit

Answer 1

Calculus books 263

History Books 131

Marketing Books 656

Total Profit will be $8,402

Step-by-step explanation:

There are 3 different types of books which can be purchased from the student run used book program. History book occupies 1 unit, Calculus book occupies 2 units and Marketing text occupies 5 units. There is budget constraint on purchase of books and maximum 1040 can be purchased. Lets formulate an equation for the books to identify the profit.

Constraint equation is :

h + 2c + 5m
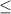`\leq` 1050

Profit equation is :

P = 4h + 10c + 8m

The total ratio is 2 + 5 + 1 = 8

Calculus books : 2 / 8 * 1050 = 263

History Books : 1 / 8 *1050 = 131

Marketing books : 5 / 8 * 1050 = 656

The maximum number of books purchase is inserted into the profit equation to identify maximum profit.

P = 4 * 131 + 10 * 263 + 8 * 656

P = $8,402