Question

The human resources department of an engineering company gives IQ tests to a randomly selected group of new hires every year. They claimed that the mean IQ score of new hires, , from this year is greater than or equal to the mean IQ score of new hires, , from last year. This year, 95 new hires took the test and scored an average of 112.2 points with a standard deviation of 14.0 . Last year, 70 new hires took the IQ test and they scored an average of 117.8 points with a standard deviation of 14.5 . Assume that the population standard deviation of the IQ scores from the current year and the last year can be estimated by the sample standard deviations, since the samples that are used to compute them are quite large. Is there enough evidence to reject the claim of the human resources department, at the 0.01 level of significance

Answer 1

Explanation:

Null hypothesis:
`\mathbf{H_o: \mu_1 \ge \mu_2}`

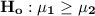
Alternative hypothesis:
`\mathbf{H_o: \mu_1< \mu_2}`

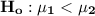
This type of test statistic is a z test statistics

1st 2nd

Sample mean x = 112.2 117,8

Standard deviation σ = 14.0 14.5

Sample size n = 95 70

Point estimate
`\bar x_1 - \bar x_2` = -5.60

Standard error
`\sigma_(x_1-x_2)= \sqrt{(\sigma_1^2)/(n_1) +(\sigma_2^2)/(n_2) }`

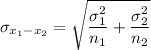
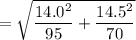`= \sqrt{(14.0^2)/(95) +(14.5^2)/(70) }` = 2.2509

Test statistics
`z=(x_1 - x_2)/(\sigma_(x_1-x_2))`
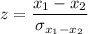
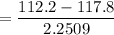`=(112.2- 117.8)/(2.2509)` = - 2.4878

P-value = 0.012

No, there is no enough evidence Since p-value is greater than 0.01.