Answer:
We reject the null hypothesis, and accept the alternative hypothesis.
So, it means that the machine is under filling the bags
Explanation:
Given
Null Hypothesis
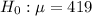 --- works correctly at 419g
--- works correctly at 419g
Alternate Hypothesis
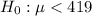 --- under fills the bag
--- under fills the bag
 --- the sample
--- the sample
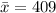 --- the mean
--- the mean
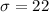 --- the standard deviation
--- the standard deviation
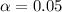 --- the significance level
--- the significance level
Required
What is the decision rule
Since n is less than 30, we make use of t test
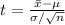
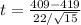
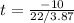


Calculate df

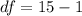
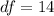
Calculate the p value from the Student's t-distribution at df = 14 and

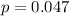
Given that:
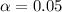
Since
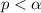
So, it means that the machine is under filling the bags