Answer:
![\displaystyle (d)/(dx)[e^(2x)] = 2e^(2x)](https://img.qammunity.org/2022/formulas/mathematics/college/1imqjn8t7osesvo9ghim8vmwymgs3jvgbt.png)
![\displaystyle (d)/(dx)[e^(3x)] = 3e^(3x)](https://img.qammunity.org/2022/formulas/mathematics/college/t1pzc57wrlnf22b276z6ny3a2dzheppi8q.png)
General Formulas and Concepts:
Algebra I
- Terms/Coefficients
- Exponential Rule [Multiplying]:
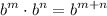
Calculus
Derivatives
Derivative Notation
eˣ Derivative:
![\displaystyle (d)/(dx)[e^x] = e^x](https://img.qammunity.org/2022/formulas/mathematics/college/qlpvo5lrrvw5uykvnjerv76dtlvddnm00x.png)
Derivative Rule [Product Rule]:
![\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)](https://img.qammunity.org/2022/formulas/mathematics/college/c6fshhoq1mws6w0d0la17c7k2dcytwd8kg.png)
Explanation:
Step 1: Define
![\displaystyle (d)/(dx)[e^(2x)] = (d)/(dx)[e^x \cdot e^x]](https://img.qammunity.org/2022/formulas/mathematics/college/iws8m55r5ew2z6u46lyar0hqsw14cthffz.png)
![\displaystyle (d)/(dx)[e^(3x)] = (d)/(dx)[e^x \cdot e^(2x)]](https://img.qammunity.org/2022/formulas/mathematics/college/td96kl5p6pn1q9tytlsbbw7f81j05dpzjc.png)
Step 2: Differentiate
![\displaystyle (d)/(dx)[e^(2x)]](https://img.qammunity.org/2022/formulas/mathematics/college/xa8i0iv0pg8pvpikntu0bebfhe5wbajt4z.png)
- [Derivative] Product Rule:
![\displaystyle (d)/(dx)[e^(2x)] = (d)/(dx)[e^x]e^x + e^x(d)/(dx)[e^x]](https://img.qammunity.org/2022/formulas/mathematics/college/2udtx23da7bj7x8yd65sc2yn7iwpe5vlla.png)
- [Derivative] eˣ Derivative:
![\displaystyle (d)/(dx)[e^(2x)] = e^x \cdot e^x + e^x \cdot e^x](https://img.qammunity.org/2022/formulas/mathematics/college/nhe5ntbi8xe7b6kwlxhvnqx9bk3y6ectqe.png)
- [Derivative] Multiply [Exponential Rule - Multiplying]:
![\displaystyle (d)/(dx)[e^(2x)] = e^(2x) + e^(2x)](https://img.qammunity.org/2022/formulas/mathematics/college/t6xvxbez7hoq8wntfticxp2m0ncdjm3t3e.png)
- [Derivative] Combine like terms [Addition]:
![\displaystyle (d)/(dx)[e^(2x)] = 2e^(2x)](https://img.qammunity.org/2022/formulas/mathematics/college/1imqjn8t7osesvo9ghim8vmwymgs3jvgbt.png)
![\displaystyle (d)/(dx)[e^(3x)]](https://img.qammunity.org/2022/formulas/mathematics/college/aqobrcljxxnwhkb24f9k5b7lgcc7dreeif.png)
- [Derivative] Product Rule:
![\displaystyle (d)/(dx)[e^(3x)] = (d)/(dx)[e^x]e^(2x) + e^x(d)/(dx)[e^(2x)]](https://img.qammunity.org/2022/formulas/mathematics/college/zeeq3167m1xrvwqub8exwut40i2mk49t2r.png)
- [Derivative] eˣ Derivatives:
![\displaystyle (d)/(dx)[e^(3x)] = e^x(e^(2x)) + e^x(2e^(2x))](https://img.qammunity.org/2022/formulas/mathematics/college/9uke190qttsrlcxkdql8vt04p3p2iv6wdw.png)
- [Derivative] Multiply [Exponential Rule - Multiplying]:
![\displaystyle (d)/(dx)[e^(3x)] = e^(3x) + 2e^(3x)](https://img.qammunity.org/2022/formulas/mathematics/college/mc5w2d9xsrpzm61dvmz3tz4j0gv7ju5iho.png)
- [Derivative] Combine like terms [Addition]:
![\displaystyle (d)/(dx)[e^(3x)] = 3e^(3x)](https://img.qammunity.org/2022/formulas/mathematics/college/t1pzc57wrlnf22b276z6ny3a2dzheppi8q.png)
Topic: AP Calculus AB/BC (Calculus I/II)
Unit: Derivatives
Book: College Calculus 10e