Answer:
The maintance cost and the value will be the same in 9 years.
Explanation:
Exponential function:
An exponential function has the following format:

In which r is the rate of change.
The value starts at $20,000 and decreases by 15% each year.
This means that
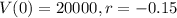
So
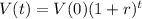
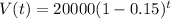
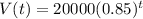
The maintance cost is $500 the first year and increases by 28% per year.
This means that
 . So
. So
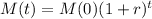

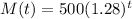
When will the maintenance cost and the value be the same.
This is t for which:
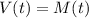
So


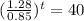
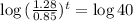
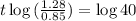
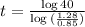

The maintance cost and the value will be the same in 9 years.