Question

A researcher reports that 80% of high school seniors would pass a driving test, but only 45% of high school freshmen would pass the same driving test. Assume that the researcher’s claim is true. Suppose a driving test is given to a random sample of 90 high school seniors and a separate random sample of 85 high school freshmen. Let and be the sample proportions of seniors and freshmen, respectively, who pass the test. What are the shape and mean of the sampling distribution of ? skewed left with mean –0.35 skewed right with mean 0.625 exactly Normal with mean 0.35 approximately Normal with mean 0.35 approximately Normal with mean 0.625

Answer 1

approximately Normal with mean 0.35

Explanation:

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

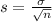For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
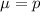`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

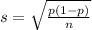
A researcher reports that 80% of high school seniors would pass a driving test, but only 45% of high school freshmen would pass the same driving test.

This means that
`p_1 = 0.8, p_2 = 0.45`

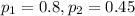
Subtraction of Variable 1 by Variable 2:

By the Central Limit Theorem, the shape will be approximately normal.

The mean is the subtraction of the means of each proportion. So

`p = p_1 - p_2 = 0.8 - 0.45 = 0.35`

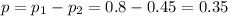
So the correct answer is given by:

approximately Normal with mean 0.35