Answer:
The variable of interest is the proportion of flips that land the correct way when flipped randomly.
The necessary conditions
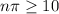 and
and
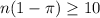 are present.
are present.
The 98% confidence interval for the overall proportion of bottles that land correctly when flipped randomly is (0.131, 0.167).
Explanation:
Variable of Interest:
Proportion of flips that land the correct way when flipped randomly.
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
Necessary conditions:
The necessary conditions are:
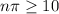
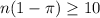
You observe 2180 random, independent flips, and 325 land the correct way.
This means that
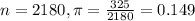
Necessary conditions
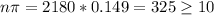
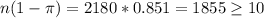
The necessary conditions
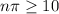 and
and
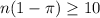 are present.
are present.
98% confidence level
So
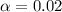 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
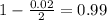 , so
, so
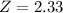 .
.
The lower limit of this interval is:
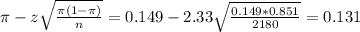
The upper limit of this interval is:

The 98% confidence interval for the overall proportion of bottles that land correctly when flipped randomly is (0.131, 0.167).