Answer:
∠A=26º
∠B=137º
∠C=17º
Explanation:
We can use the Law of Cosines because we have all 3 side lengths.
cosA =

cosA=28^2+12^2-18^2 / 2(28)(12)
cosA=604/672
cos-1(604/672
angle A ≈ 26º
cosB =
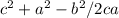
cosB=-316/432
cos-1(-316/432
angle B ≈ 137º
26+137=163
180-163=17
angle C ≈ 17º