Question

An airline finds that if it prices a cross-country ticket at $200, it will sell 300 tickets per day. It estimates that each $20

price reduction will result in 50 more tickets sold per day. Find the ticket price (and the number of tickets sold) that will
maximize the airline's revenue.
ticket price?
number of tickets?

Answer 1

We can write that as a function:

`f(n)=(200 -20n) * (300 + 50n)\\f(n)=60000+10000n-6000n-1000n^2\\f(n)=-1000n^2+4000n+60000\\`

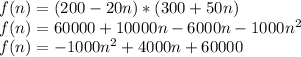
where
`n` is the number of price reductions. We can see that it is a quadratic function which has the biggest value at P = (p, q). It means that p is the number of reductions which results in the biggest profit.

`p=(-b)/(2a)=(-4000)/(-2000)=2`

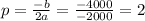
It means that it's the best to make 2 price reductions for the company. The tickets should be sold for $200 - 2 * $20 = $160. It results in 2 * 50 more tickets sold which is 300 + 100 = 400.

Answer:

Ticket price: $160

Number of tickets: 400