Answer:
D₁ = 3.31 m
D₂ = 0.9 m
Step-by-step explanation:
First, we will find the scaling factor of the model:
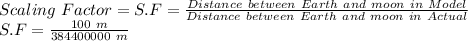
S.F = 2.6 x 10⁻⁷
Now, the diameter of 1st sphere, that is Earth will be:
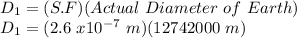
D₁ = 3.31 m
Now, the diameter of 2nd sphere, that is Moon will be:
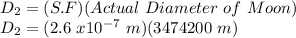
D₂ = 0.9 m