The cosine equation is
![\[ f(x) = 6\cos(x - \pi) + 2 \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/yx1g3mzwv3m1x1d3zsqbmcbuecelh8we3v.png)
To find the cosine equation of the function shown in the image, we follow these steps:
1. Identify the Amplitude: The amplitude of a trigonometric function is the distance from the midline of the graph to a peak or trough. From the graph, we can see that the maximum value is 8 and the minimum is -4. Therefore, the amplitude is
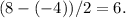
2. Determine the Period: The period of a trigonometric function is the distance along the x-axis to complete one full cycle. On the graph, one full cycle appears to go from 0 to
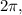 which is typical for the sine and cosine functions without any horizontal stretch or compression.
which is typical for the sine and cosine functions without any horizontal stretch or compression.
3. Calculate the Phase Shift: The phase shift is the horizontal movement of the function. A cosine function starts at its maximum value. By observing the graph, it seems the first maximum point from the y-axis is at
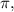 which indicates a phase shift of
which indicates a phase shift of
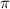 to the right.
to the right.
4. Determine the Vertical Shift: This is the movement of the function up or down on the graph. The midline of the function appears to be at y = 2 , because that's halfway between the maximum of 8 and the minimum of -4. So there is a vertical shift of 2 units up.
5. Formulate the Function: A general cosine function can be written as:
![\[ f(x) = A\cos(B(x - C)) + D \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/2l5ifvuc2v8ow2pc7nhtqammad6ea7woyw.png)
where A is the amplitude,
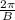 is the period, C is the phase shift, and D is the vertical shift.
is the period, C is the phase shift, and D is the vertical shift.
Given our observations:
- Amplitude A = 6
- Period
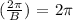 (since there is no horizontal stretch, B = 1
(since there is no horizontal stretch, B = 1
- Phase Shift C =
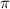
- Vertical Shift D = 2
Plugging these into the general form gives us:
![\[ f(x) = 6\cos(x - \pi) + 2 \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/yx1g3mzwv3m1x1d3zsqbmcbuecelh8we3v.png)
This would be the cosine equation of the function shown on the graph. The function has an amplitude of 6, no horizontal stretch (since the period is
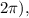 a phase shift to the right by
a phase shift to the right by
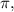 and a vertical shift upwards by 2.
and a vertical shift upwards by 2.