Answer:
Explanation:
From the given question; we can use the R software to program the combination function that generates all the combinations.
options(digits =2(
scores<- c(68,77,82,85,53,64,71)
groupA <- combn(scores,4)
groupB <- apply(groupA,2, function(x) scores[! (scores %in% x) ] )
colnames(groupA) <- colnames(groupB) <- paste("G", 1:35, sep"")
The accompanying 35 groupings (G1 to G35) contain all potential ways these understudies can be randomized under the null hypothesis
Group A
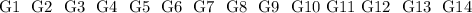



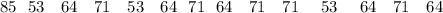
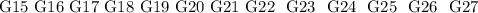
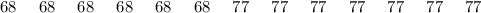
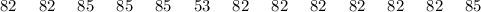
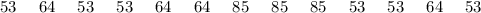
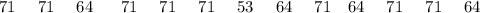

Group B

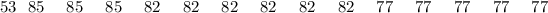
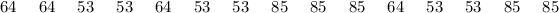
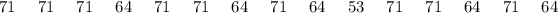
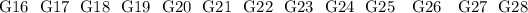
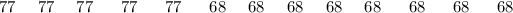
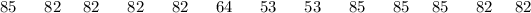
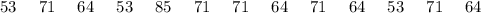

The accompanying data below computes the distinctions for each group:
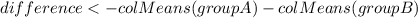

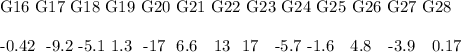

The two-sided p-value is the extent of contrasts between test midpoints as large or bigger in supreme value than the primary group. The cat function makes the outcomes simpler to peruse.
p <- sum (aba(difference)>=difference[1])/35
cat(p)
= 0.086