Question

The probability that a person fails to meet CDC Physical Activity Guidelines for both aerobic and muscle-strengthening activity is 0.77. The probability that a person eats a poor diet based on the American Heart Association healthy diet score is.48. The probability that a person fails to meet the Physical Activity Guidelines and eats a poor diet is.42.

a. What is the probability that a randomly selected person fails to meet the activity guidelines or eats a poor diet?
b. Find the probability that a randomly selected person is leading a healthy lifestyle. That is, they meet the Physical Activity Guidelines and eat a diet that is not poor. Include a Venn diagram in your response.
c. If you randomly select 4 people, what is the probability that they all eat a poor diet assuming independence?
d. If you randomly select 3 people, what is the probability that the first one meets the Physical Activity Guidelines and the last two do not?

Answer 1

a) the probability that a randomly selected person fails to meet the activity guidelines or eats a poor diet is 0.83

b) the probability that a randomly selected person is leading a healthy lifestyle is 0.17

c) the probability that they all 4 people eat a poor diet assuming independence is 0.05308

d) the probability that the first one meets the Physical Activity Guidelines and the last two do not is 0.1364

Step-by-step explanation:

Given the data in the question;

Let E represent the events

E1 = P( person fails to meet CDC Physical Activity Guidelines ) = 0.77

E2 = P( person eats a poor diet ) = 0.48

E3 = P(E1 ∩ E2) = P( both ) = 42

a) What is the probability that a randomly selected person fails to meet the activity guidelines or eats a poor diet?

the probability that a person eats a poor diet or fails to meet the activity guidelines will be;

P( E1 ∪ E2 ) = P(E1) + P(E2) - P(E1 ∩ E2)

so we substitute

P( E1 ∪ E2 ) = 0.77 + 0.48 - 0.42 = 0.83

Therefore, the probability that a randomly selected person fails to meet the activity guidelines or eats a poor diet is 0.83

b) Find the probability that a randomly selected person is leading a healthy lifestyle. That is, they meet the Physical Activity Guidelines and eat a diet that is not poor?

In the light of De-Morgan’s Laws

P(
`E_1^c` ∩
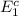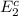`E_2^c` ) = 1 - P( E1 ∪ E2 )

so

P(
`E_1^c` ∩
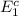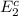`E_2^c` ) = 1 - 0.83 = 0.17

Therefore, the probability that a randomly selected person is leading a healthy lifestyle is 0.17

c) If you randomly select 4 people, what is the probability that they all eat a poor diet assuming independence?

if we select 4 people;

E2 = P( person eats a poor diet ) = 0.48

so

P = ( 0.48 )⁴ = 0.05308

Therefore, the probability that they all 4 people eat a poor diet assuming independence is 0.05308

d) If you randomly select 3 people, what is the probability that the first one meets the Physical Activity Guidelines and the last two do not?

we select 3 people;

P( person fails to meet CDC Physical Activity Guidelines ) = 0.77

P( person meet CDC Physical Activity Guidelines ) = 1 - 0.77 = 0.23

so

P = 0.23 × ( 0.77)²

P = 0.1364

Therefore, the probability that the first one meets the Physical Activity Guidelines and the last two do not is 0.1364