Question

Factor the greatest common factor from the polynomial 3x^2 + 6x -9

Answer 1

`3(x+3)(x -1)`

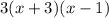
Explanation:

`3x^2 + 6x -9`

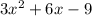
All the terms in this polynomial are divisible by 3. Factor 3 out of this polynomial:

`= 3(x^2 + 2x -3)`

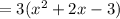
Now, factor inside the parentheses by grouping:

`= 3(x^2 -1x+3x -3)`

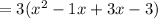
We knew to split the +2x up into -1x and 3x because -1 and 3 multiply to get -3, which is the last value in the polynomial.

`= 3(x(x -1)+3(x -1))\\= 3(x+3)(x -1)`

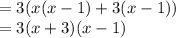
Therefore, the final factored polynomial is
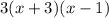`3(x+3)(x -1)`.