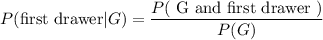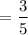Question

A cabinet has three drawers. In the first drawer there are 3 gold balls. In the second drawer there are 3 silver balls. In the third drawer there are 3 silver balls and 2 gold balls An experiment consists of choosing a drawer, and then choosing a ball inside it. Each drawer is equally likely to be chosen, and within each drawer, each ball is equally likely to be chosen. For example, P(A gold ball is chosen | Drawer 3 is chosen) 2/5 Given that a gold ball is chosen, what is the probability that the drawer with 3 gold balls was selected? Now what if all the balls are numbered from 1-3 based on which drawer they were in, and then taken from the drawers and placed into a large pile of 11 balls? Each ball in this pile is now equally likely to be chosen, unlike in the previous part. Given that a gold ball is chosen, what is the probability that the gold ball came from the drawer with 3 gold balls?

Answer 1

Let
`$D_1,D_2,D_3$` be the events that the first, second and the third drawers are selected respectively.

Therefore,
`$P(D_1)=P(D_2)=P(D_3)=(1)/(3)$`

Now the G shows that the events that the gold ball is selected, so

`$P(G|D_1)=1,P(G|D_2)=0,P(G|D_3)=(2)/(5),$`

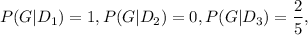
By probability, he gold ball is selected is :

`$P(G)=P(G|D_1)P(D_1)+P(G|D_2)P(D_2)+P(G|D_3)P(D_3)$`

`$=1.(1)/(3)+0.(1)/(3)+(2)/(5).(1)/(3)$`

`$=(7)/(15)$`

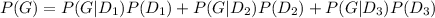
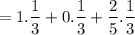
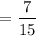
Now the required probability is :

`$P(D_1|G)=(P(G|D_1)P(D_1))/(P(G))$`

`$=(1/3)/(7/15)$`

`$=(5)/(7)$`

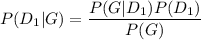
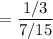
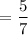
= 0.71

Now out of 11 balls, 3+2 = 5 balls are gold balls.

Therefore,
`$P(G)=(5)/(11)$`

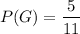
The probability that a gold ball and the first drawer is selected is :

`$P(G \text{ and first drawer})= (3)/(11)$`

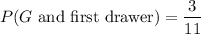
Now the required probability is :

`$P(\text{first drawer}|G)=\frac{P(\text{ G and first drawer })}{P(G)}$`

`$=(3/11)/(5/11)$`

`$=(3)/(5)$`